\[X_{k} = \sum_{k=0}^{N-1} e^{-2\pi i k / N} x_i\]

FFTW is a popular C-library for computing the discrete Fourier transform and its documentation page provides comprehesive information on the library. For Python, pyFFTW provides an excellent wrapper. Below, we show a simple example in both C and Python versions to illustrate how the Python wrapper corresponds to the actual library.

Example

The example does the follow calls:

allocate spaces for x, y, and z (z_N in C version), each of which has N complex numbers.
set up fft and ifft plans.
- fft: from x to y
- ifft: from y to z (z_N in C version)
fill x with cos(3 * pi * t) and call fft to get y.
fill x with cos(5 * pi * t) and call fft to get a different y.
call ifft on y to get z (z_N in C version)
compared to x.
- In C, z_N is the same to x * N because the library does not include the scale factor.
- In Python, z is the same to x because the wrapper adds the scale factor.

Both versions together

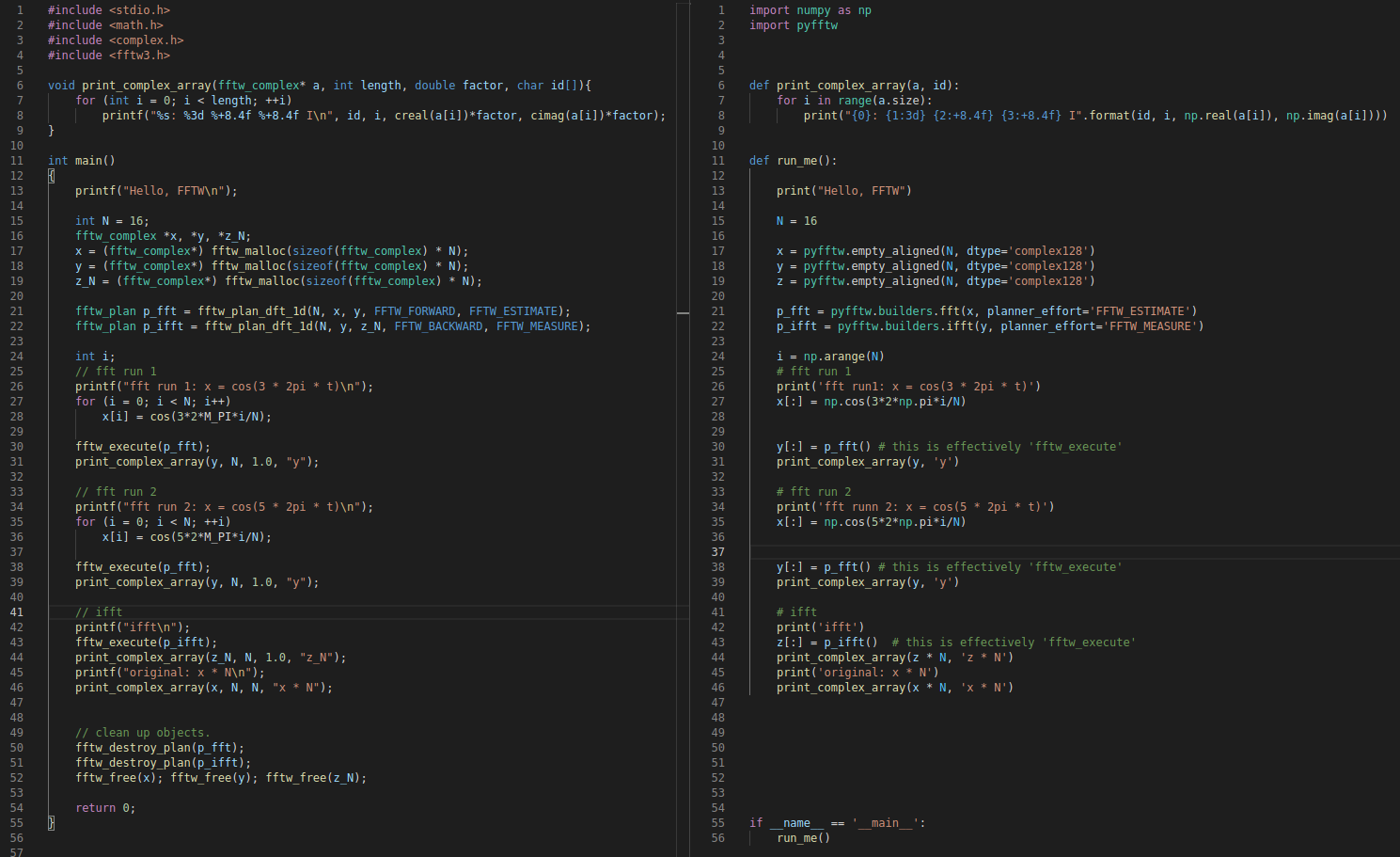
To see both versions together, click the image below. The left panel is in C and the right panel is in Python. Extra spaces are added to the Python version so that the two versions are aligned line-by-line.

Codes: C

#include <stdio.h>
#include <math.h>
#include <complex.h>
#include <fftw3.h>

void print_complex_array(fftw_complex* a, int length, double factor, char id[]){
    for (int i = 0; i < length; ++i)
        printf("%s: %3d %+8.4f %+8.4f I\n", id, i, creal(a[i])*factor, cimag(a[i])*factor);
}

int main()
{
    printf("Hello, FFTW\n");
    
    int N = 16;
    fftw_complex *x, *y, *z_N; 
    x = (fftw_complex*) fftw_malloc(sizeof(fftw_complex) * N);
    y = (fftw_complex*) fftw_malloc(sizeof(fftw_complex) * N);
    z_N = (fftw_complex*) fftw_malloc(sizeof(fftw_complex) * N);
    
    fftw_plan p_fft = fftw_plan_dft_1d(N, x, y, FFTW_FORWARD, FFTW_ESTIMATE);
    fftw_plan p_ifft = fftw_plan_dft_1d(N, y, z_N, FFTW_BACKWARD, FFTW_MEASURE);

    int i;
    // fft run 1
    printf("fft run 1: x = cos(3 * 2pi * t)\n");
    for (i = 0; i < N; i++)
        x[i] = cos(3*2*M_PI*i/N);
    
    fftw_execute(p_fft);
    print_complex_array(y, N, 1.0, "y");

    // fft run 2
    printf("fft run 2: x = cos(5 * 2pi * t)\n");
    for (i = 0; i < N; ++i)
        x[i] = cos(5*2*M_PI*i/N);
    
    fftw_execute(p_fft);
    print_complex_array(y, N, 1.0, "y");

    // ifft
    printf("ifft\n");
    fftw_execute(p_ifft);
    print_complex_array(z_N, N, 1.0, "z_N");
    printf("original: x * N\n");
    print_complex_array(x, N, N, "x * N");


    // clean up objects. 
    fftw_destroy_plan(p_fft);
    fftw_destroy_plan(p_ifft);
    fftw_free(x); fftw_free(y); fftw_free(z_N);

    return 0;
}

Codes: Python

import numpy as np
import pyfftw

def print_complex_array(a, id):
    for i in range(a.size):
        print("{0}: {1:3d} {2:+8.4f} {3:+8.4f} I".format(id, i, np.real(a[i]), np.imag(a[i])))

def run_me():

    print("Hello, FFTW")

    N = 16

    x = pyfftw.empty_aligned(N, dtype='complex128')
    y = pyfftw.empty_aligned(N, dtype='complex128')
    z = pyfftw.empty_aligned(N, dtype='complex128')

    p_fft = pyfftw.builders.fft(x, planner_effort='FFTW_ESTIMATE')
    p_ifft = pyfftw.builders.ifft(y, planner_effort='FFTW_MEASURE')

    i = np.arange(N)
    # fft run 1
    print('fft run1: x = cos(3 * 2pi * t)')
    x[:] = np.cos(3*2*np.pi*i/N)

    y[:] = p_fft() # this is effectively 'fftw_execute'
    print_complex_array(y, 'y')

    # fft run 2
    print('fft runn 2: x = cos(5 * 2pi * t)')
    x[:] = np.cos(5*2*np.pi*i/N)

    y[:] = p_fft() # this is effectively 'fftw_execute'
    print_complex_array(y, 'y')
    
    # ifft
    print('ifft')
    z[:] = p_ifft()  # this is effectively 'fftw_execute'
    print_complex_array(z * N, 'z * N')
    print('original: x * N')
    print_complex_array(x * N, 'x * N')

if __name__ == '__main__':
    run_me()