Deribit provides public APIs to request market data of options on crypto currencies including BTC and ETH. Since cryptos are currencies, let’s look for risk reversals and butterflies. Nothing new other than applying standards from the FX market and doing my own revisions on the subject (jupyter notebook - needs clean-up).

Using the APIs, download option market data (see a simple code in the notebook). The data include greeks including deltas. ETH option data are used below.

Strikes to Delta-based Tenors

For illustration purposes, fix a specific expiry date.

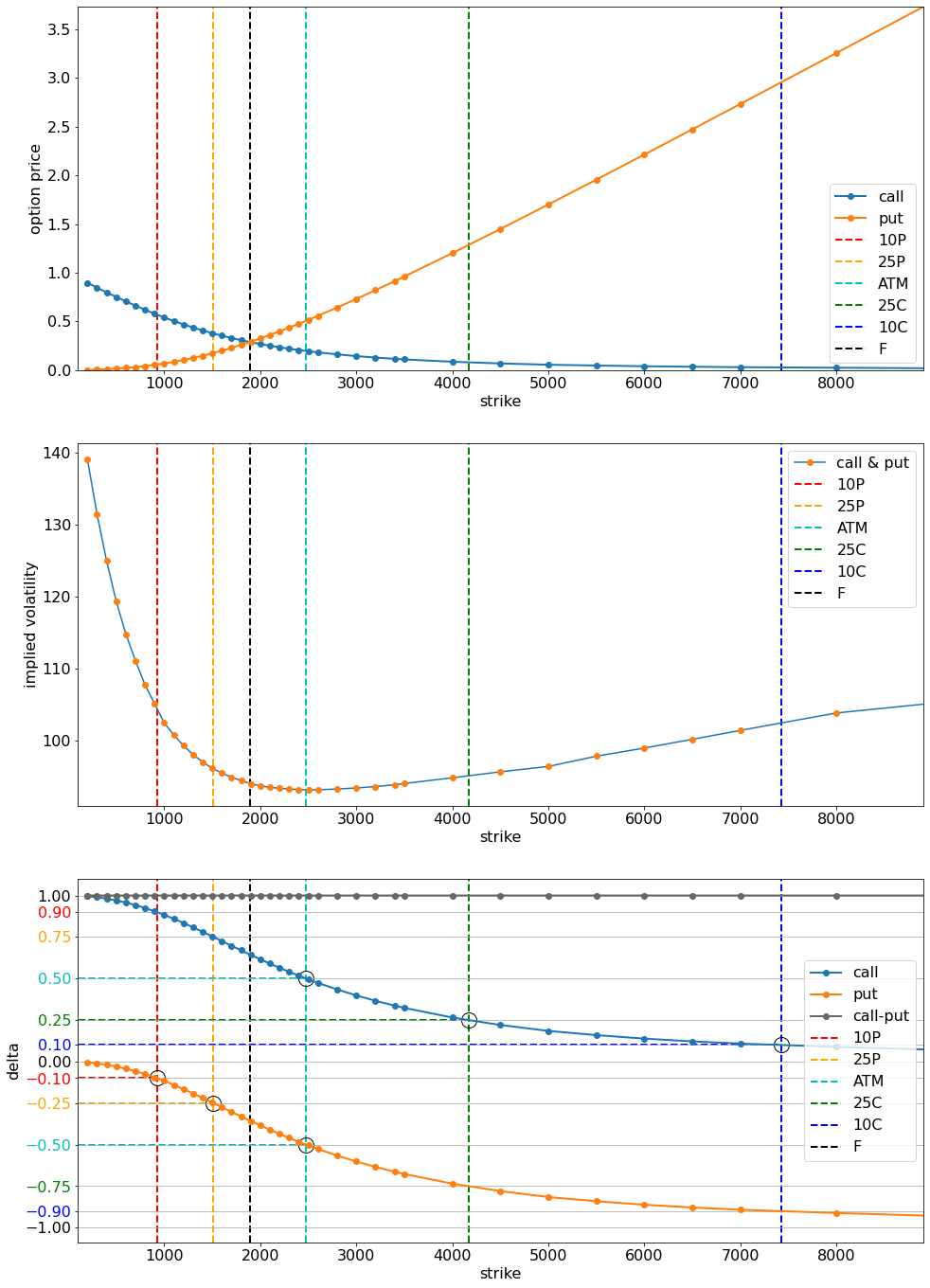
  • The first plot below shows option prices of call (blue) and put (orange) instruments in terms of strikes.

    • The black vertical dashed-line corresponds to the underlying price in the data. The well-known parity

      \[C(F, K) - P(F,K) = \mathrm{DF} \times (F - K)\]

      implies that it is the forward rate $F$ for this expiry.

    • Each of the 5 colour vertical dashed-lines is the strike value corresponding to a certain delta amount, as discussed below.

  • The second plot shows implied volatilities across strikes. Due to the parity relationship, the volatility levels do not depend on the option type.

  • The third plot shows delta sensitivities across strikes by option type. From the parity equation, we have

    \[\delta_{C}(K) - \delta_{P}(K) = 1\]

    As illustrated in the figure, we calculate the following strike values

    \[{\color{red} K_{10P}}, {\color{orange} K_{25P}}, {\color{cyan} K_{\mathrm{ATM}}}, {\color{green} K_{25C}}, {\color{blue} K_{10C}}\]

    by interpolating delta sensitivity curves as below:

    • At-the-money (ATM)$:
    \[\delta_{C}(K_{\mathrm{ATM}}) = 50\% = -\delta_{C}(K_{\mathrm{ATM}})\]
    • Right wing: $xC$:
    \[\delta_{C}(K_{xC}) = x\%,\quad\textrm{or equivalently},\quad = \delta_{P}(K) = (x-100)\%.\]
    • Left wing: $xP$:
    \[\delta_{P}(K_{xP}) = -x\%,\quad\textrm{or equivalently},\quad = \delta_{C}(K) = -(x-100)\%.\]

plot

Risk-Reversal and Butterfly

For a given delta $x$, the risk-reversal and butterfly volatility parameters are defined as

\[\begin{eqnarray*} \sigma(K_{x\mathrm{RR}}) &=& \sigma(K_{xC}) - \sigma(K_{xP})\\ \\ \sigma(K_{x\mathrm{FLY}}) &=& \frac{\sigma(K_{xC}) + \sigma(K_{xP})}{2} - \sigma(K_{\mathrm{ATM}}) \end{eqnarray*}\]

TODOs

  • think about extrapolation
  • show an iv matrix
  • confirm Deribit’s risk sensitivity calculations