Catalan Triangle - Alternative Proof

Random Walk and Back to Origin

Consider a random walk with 50/50 chance to go up/down by a unit. Let \(X_n\) be the location after $n$-th step with $X_0 = 0$. How many ways are there to come back to the original location at the $2n$-th step with

\begin{equation} X_j > 0 \text{ for }j = 1, \cdots, 2n-1 \label{E:condition} \end{equation} in other words, while staying positive? The answer to this question is known to be the $\color{red}{(n-1)}$-the Catalan number.

Whilst there are many ways to prove this, I would like to present my way as an alternative.

Let’s consider Pascal’s triangle where the $k$-th element of the $n$-th row is given by \begin{equation} P(n,k) = \left( \begin{array}{c} n \\ k \end{array} \right) \nonumber \end{equation} where $n = 0, 1, \cdots, $ and $k = 0, 1, \cdots, n$.

The triangle can be depicted as below

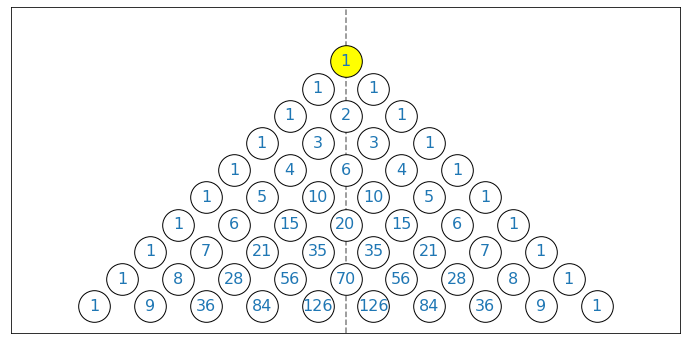
where $n = 0$ corresponds to the top row and $k=0$ corresponds to the far left circle in each row.

The triangle is thought to be constructed by

1. fill the space with zeros: $P(n,k) = 0$ for $n$ and $k$ all integers (negative integers as well)
2. drop one at the yellow circle: $P(0,0) = 1$
3. let it cascade down through \begin{equation} P(n,k) = P(n-1, k-1) + P(n-1, k) \nonumber \end{equation}
4. update $n \leftarrow n+1$ and go back to step 3.

If condition (\ref{E:condition}) can be ignored, the triangle tracks the number of possible paths to each circle from the starting yellow circle with

left half	center line	right half
$\color{blue}{X_n} > 0$	$X_n=0$	$\color{red}{X_n} < 0$

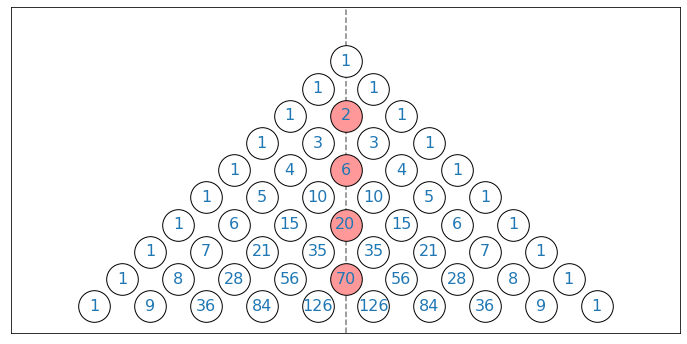
Catalan’s Triangle

Condition (\ref{E:condition}) can be incorporated by adding the step between step 3 and 4: (step 3.5): If $n$ is even, overwrite the value (red circles below) at the center to zero \begin{equation} P(n, n/2) \leftarrow 0 \end{equation}

The same result can be achieved if we reverse the sign of the values in the right half and perform the standard Pascal triangle operation without overwriting.

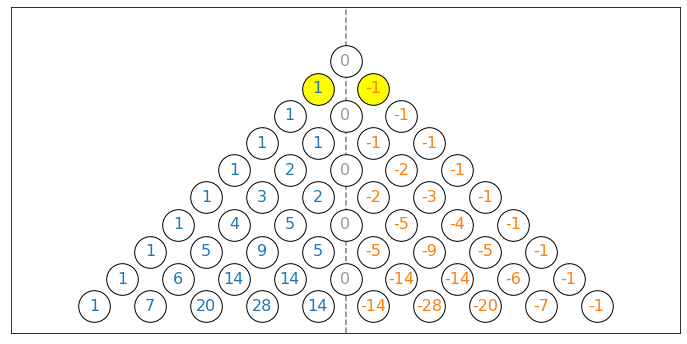
This triangle is the sum of the two Pascal’s triangles starting from the yellow circles above, respectively.

	triangle 1	triangle 2
constructed by	dropping +1 at (1,0) at step 2	dropping -1 at (1,1) at step 2
value	$P_1(n,k) = \left( \begin{array}{c} n-1 \\ k \end{array} \right) $	$P_2(n,k) = -\left( \begin{array}{c} n-1 \\ k-1 \end{array} \right)$

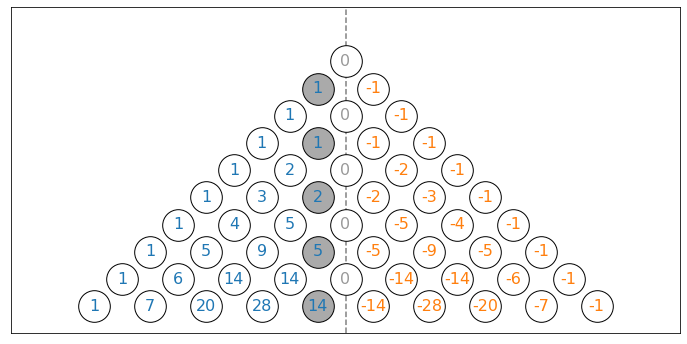
Then, the number of possible paths to return to zero at $2n$ is the value at (2n-1, n-1) as highlighted in grey, i.e. 1, 1, 2, 5, 14, … \begin{equation} P_1(2n-1, n-1) + P_2(2n-1,1) = \left( \begin{array}{c} 2(n-1) \\ (n-1) \end{array} \right)- \left( \begin{array}{c} 2(n-1) \\ (n-1)-1 \end{array} \right) = C(n-1) \end{equation}